コロナも第4波が京都ではやや沈静化しつつありますがまた行動制限を緩めると再拡大、第5波の到来が危惧されます。
一方、コロナが猛威を奮っていた欧米でも収束しつつあることを考えるとワクチンの有効性は疑いようがないように考えます。
感染症数理モデルにワクチン接種率を組み込んだモデルで平易なものが無いので解説、シミュレーションを行ってみました。SIRモデルといわれる最もシンプルなモデルで考えてみます。
総人口 = 感受性保持者数(S) + 感染者数(I) + 免疫保持者の数(R)
S(t) = 時間 t における感受性保持者の数
I(t) = 時間 t における感染者数
R(t) = 時間 t における免疫保持者数
とした場合、S,I,Rのそれぞれの推移を下記の3つの微分方程式で考えるのがSIRモデルです。βは感染率、γは回復率を表す定数です。β/γが基本再生算数(R0)と言われます。
S’(t) = −βS(t)I(t) (1)
I’ (t) = βS(t)I(t) − γI(t) (2)
R’(t) = γI(t) (3)
*新規感染者(I’(t))が未感染者と感染者の積に比例し増加する、というところを理解すれば式の意味がつかみやすくなります。
基本再生産数を3.0と考えた場合のエピカーブは
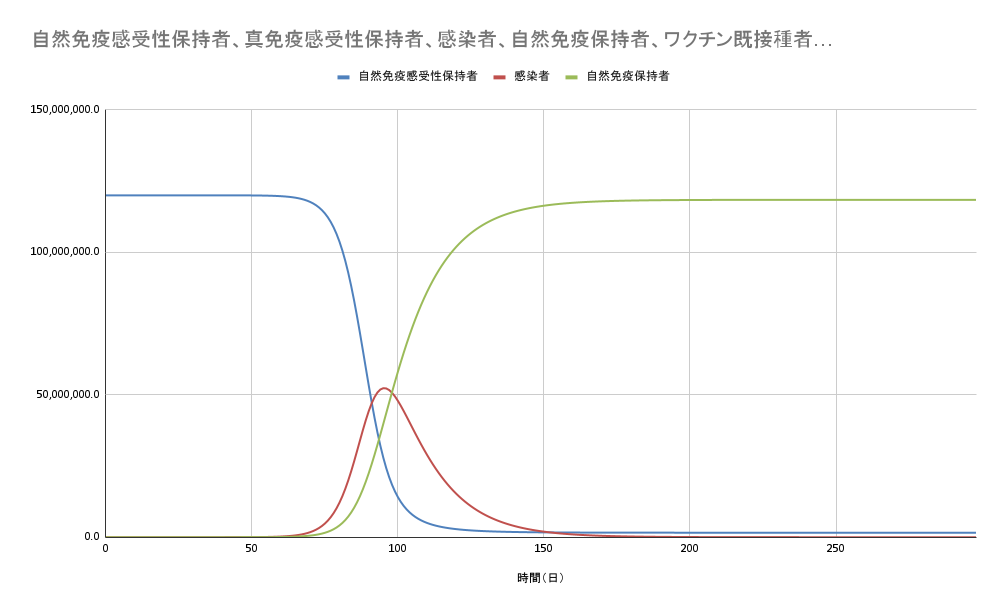
となります。行動制限をかけないと感染はかなりひろがり合計感染者数は7000万人を超えます。
ワクチン接種済数(W(t))という新しいパラメーターをここに入れ込みます。
W’(t) = ω (4)
ωは1日あたりのワクチン接種者数を示しています。そうすると前述の式は
S’(t) = −βS(t)I(t) – W(t) (1’)
I’ (t) = β(S(t)-W(t))I(t) − γI(t) (2’)
R’(t) = γI(t)+W(t) (3’)
となります。現在は政府も力を入れており40万人/日が接種しており、最終的には100万人/日の接種を目指すとされています。1日あたりのワクチン接種人数(ω)を30日目までは10000人/日、31日~60日までは200,000人/日、61日~90日までは400,000人/日、91日以降は1,000,000人/日と考えてみます。これを用いてシミュレーションしてみます。
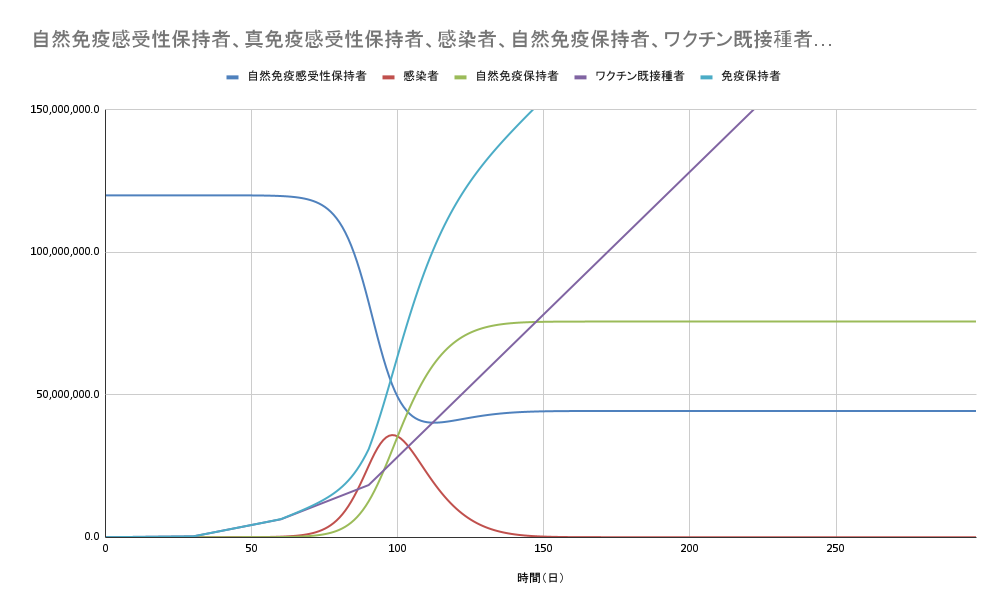
流行のピークが減っていっていることがわかると思います。もし現在の日本の1日50万人接種というワクチン接種が流行当初から行われていたとすると
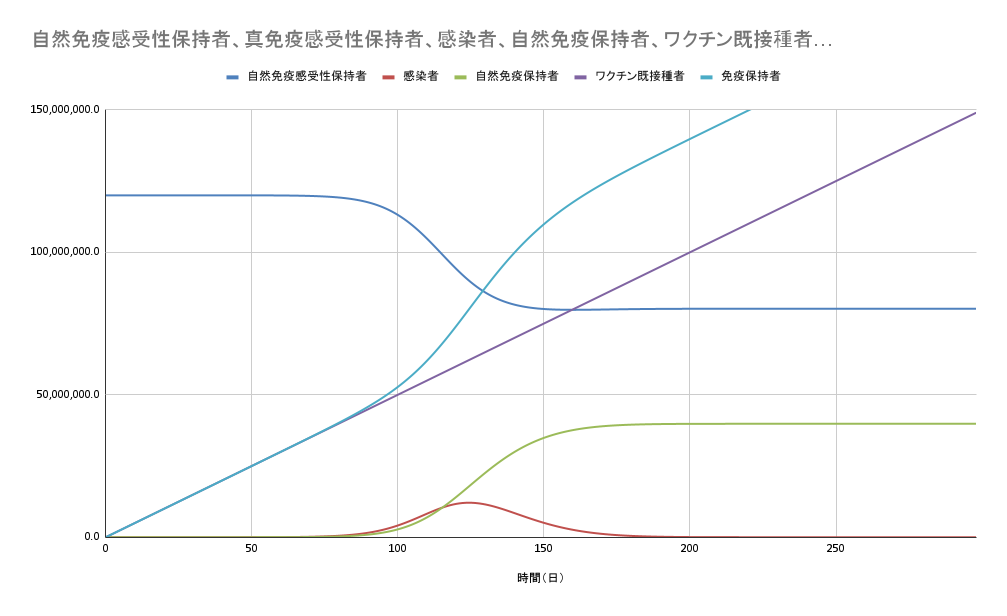
となります。さらに日本が目標に掲げている100万人/日の接種が流行当初から行われていると
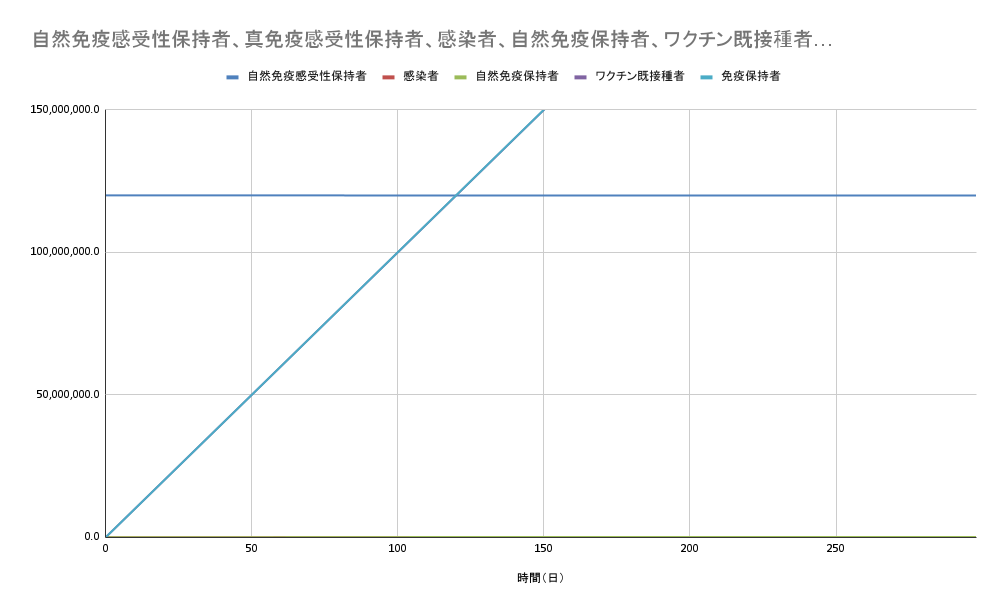
ほとんど流行が起きないというグラフになります。
少し違う方法で考えると人口×(1-1/R0)が自然免疫+ワクチンによる免疫を持てば感染は収束しますので、基本再生算数3.0とすると日本では約7200万人がワクチン接種する必要があります。現在約300万人が2回接種済み、今後、50万人/日で接種が続き、2回接種が必要とすると行動制限をしなくても感染拡大が起きなくなるのは276日後という計算になります。100万人/日で接種すると138日後という計算になります。オリンピック(開催されれば)の際は行動制限が必要ですが、冬くらいになると行動制限が緩和できる可能性はあるようです。
もちろん現実とシミュレーションは異なりますし素人の目算に過ぎません。いずれにせよ早くコロナが収束し元の日々が戻ってくることを祈っております。
googleスプレッドシートで共有しております、パラメーターを色々と変更してシミュレーションが可能です。




コメント